作者：关玉明，李祥利，苗艺男，韩晓耀

（河北工业大学机械工程学院，天津 300130）
 

1 引言

全球能源危机和环境污染，助推了新能源和可再生能源的开发利用。风能作为一种清洁的可再生资源，其储量巨大，分布广，具有取之不尽、用之不竭，不污染环境等诸多优点，已成为世界各国新能源发展的重要方向。中国是风能大国，风资源总量达20亿kW，其中陆上及近海的风资源达15亿kW，风能开发利用的潜力巨大，利用风力发电对调整能源结构、减轻环境污染、解决能源危机等有着非常重要的意义［1］。

微风根据风级定义为2 级及以下等级的风速，其风速为（0.3~3.3）m/s，传统的风电技术对于风轮切入风速，至少需要3m/s才能用于发电，对于3m/s以下的微风却无能为力，造成能源的极大浪费［2−3］。且传统的水平轴风力机发电效率大多在0.4左右，很难以达到贝兹极限0.593，如何提高风能利用率、增加风力发电机的输出功率是风能利用的关键所在。风能功率和风速的3次方成正比关系，增加风轮的风速可以有效增加风力机的输出功率［4−6］。因此，介绍一种基于文丘里效应的新型微风发电装置，在低风速地域也可充分发电，同时可将输出功率进一步提高，并对其可行性进行数值模拟仿真分析以及风洞试验。

2 高效微风发电装置的结构

2.1 微风发电原理

该高效微风发电装置，其原理通过“文丘里效应”实现风速的提高，“文丘里效应”通风原理示意图，如图1所示。气流从进风口进入，经过中间喉管后从出风口流出。根据不可压缩流连续方程：

式中：V1—进风口风速；V2—喉管部位风速；V3—出风口风速；A1—进风口横截面积；A2—喉管部位横截面积；A3—出风口横截面积；Q—流经管道的气体流量。

风通过进风口进入管道，在内部利用“文丘里效应”，文丘里管内的气流是连续的，由于A1和A3大于A2，所以喉管部位的气流速度V2大于V1和V3，在喉管部位安装风力发电机即可获得较高的风速，如图1所示。

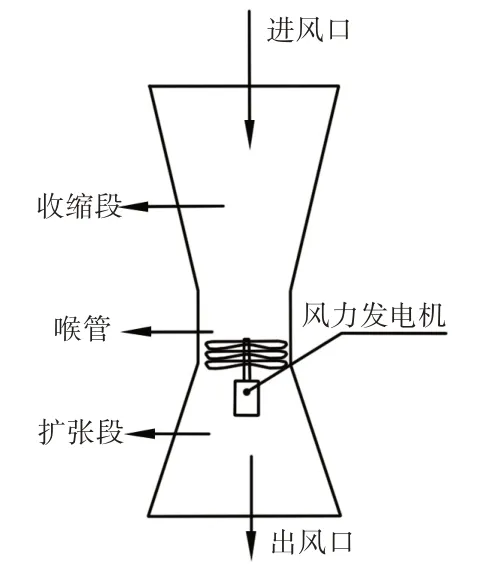
图1 “文丘里效应”通风原理示意图Fig.1 Schematic Diagram of th‘eVenturi Effect’Ventilation Principle

风进入文丘里管内，随着管道横截面积逐渐缩小，从而使风速迅速增加，使风在内部产生变化，聚集的风可使风力发电机的风轮快速转动，从而使风力发电机发电功率大大增加，达到高效微风发电的目的。当风通过风力发电机后，到达出风口位置，同样利用“文丘里效应”增加风通过的面积，从而降低出风的速度，减少了内部空气与外部空气的相对阻力，使得出风口更容易排风。

2.2 万向迎风结构

传统的水平轴风力机通过偏航系统，使风力发电机组的风轮始终处于迎风状态，以便最大限度地吸收风能，提高风力发电机组的发电效率。对小型风力机一般由尾舵实现对风，对大型风力发电机则采用电力或液压驱动的方式让机舱通过齿轮传动使风轮对准风向来完成对风动作［7］。

低速风场大多处于复杂地形区域，粗糙不平的地表降低了近地风速，且在风场中形成了大量湍流，因此，若充分利用低速风能，就必须考虑风力发电装置在风向多变环境下的适应能力。对于水平轴风力机而言，在微风状态下，对风动作缓慢而困难，其大多适用于风向相对固定的区域，且大型风力机则需要较高的启动风速。因此，对于适合利用微风发电的地域，微风发电装置需要设置万向迎风结构，来充分应对多变的风向。

具有万向迎风结构的微风发电装置三维模型，如图2所示。采用多层聚风组件，使得聚风面积大大增加，每两个聚风组件之间的连接采用等角度（30°）间隔的竖直隔板，多竖直隔板隔开的聚风组件使发电装置能够收集来自四面八方的微风，对于任意水平方向来流，都可以进入发电装置内部高效聚集发电，即万向迎风，大大增加了发电效率。

图2 万向迎风微风发电装置三维模型Fig.2 Three−Dimensional Model of Universal Windward Breeze Power Generation Device

3 高效微风发电装置的数值模拟

3.1 几何建模与网格划分

为了确保在仿真计算中能够有效进行，需要对模型进行合理简化，去除微风发电装置中的钢结构骨架，运用SolidWorks建立其简化模型，如图3所示。模型整体高度2.75m，将简化模型导入ANSYS Workbench15.0的Geomety中，并建立简化模型的流场区域，流场区域包括整个微风发电装置的流场，在模型的数值模拟中，结合实际情况，建立的整体流场区域长度12m，宽度6m，高度6m，考虑到尾流影响，来风方向流域尺寸设为4m，背风方向流域尺寸设为8m，将长方体流场区域与模型进行布尔运算，得到实际中的流体计算域。

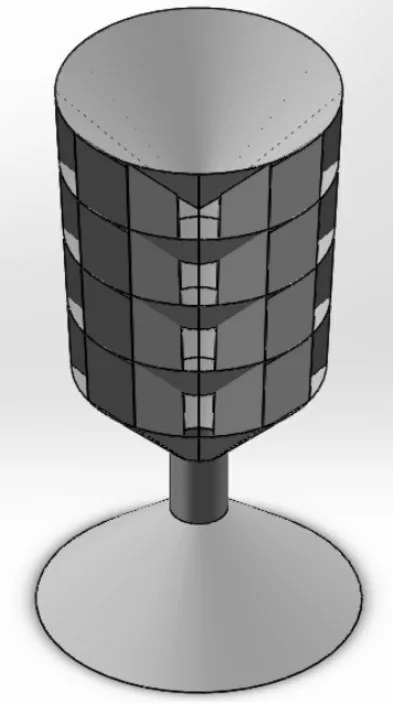
图3 简化的微风发电装置三维模型Fig.3 Simplified Three−Dimensional Model of Breeze Power Generation Device

网格划分是进行有限元数值模拟分析至关重要的一步，它直接影响数值计算分析结果的精确性，网格划分的目的是对CFD模型实现离散化，是把求解域分解成可得到精确解的适当数量的单元。利用Workbench Meshing的网格划分算法，对流体计算域划分网格，采用自由网格进行网格划分，微风发电装置模型复杂，需要在模型周围进行网格加密处理［8］。为了获得较高的网格质量，对发电装置模型表面进行膨胀处理，采用平滑过渡方式，其中过渡比0.272，最大膨胀层数5，增长率1.2。由流场区域网格划分可得，整个流场计算域的网格数为1624900，节点数为286093。流场计算域的网格划分，如图4所示。

图4 流场计算域的网格划分Fig.4 Meshing of Flow Field Calculation Domain

3.2 数学模型

假设微风发电装置模型为刚体，基于稳态不可压缩三维定常雷诺时均N−S方程（RANS）进行数值模拟，湍流模型采用重整化群模型（RNG k −ε）。

（1）雷诺平均的Navier−Stokes（RANS）方程，即控制方程：

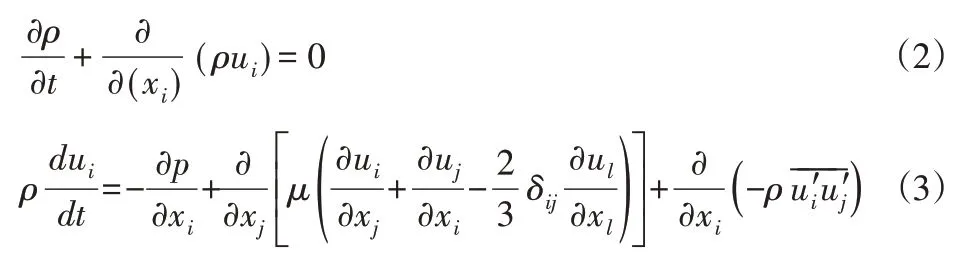
式中：ρ—气体密度；ui、uj—速度时均量；p—压力；μ—流体粘性系数；ui′、uj′—脉动速度［9］。

（2）RNG k −ε模型

采用双方程模型的RNG k −ε模型，其在处理高应变率流动时比标准k −ε模型适应性更强，并且在高应变率及流线弯曲程度较大的流场运动中有更好的效果［10］。对于不可压缩流体，RNG k −ε模型的湍动能输运方程和耗散率输运方程为：

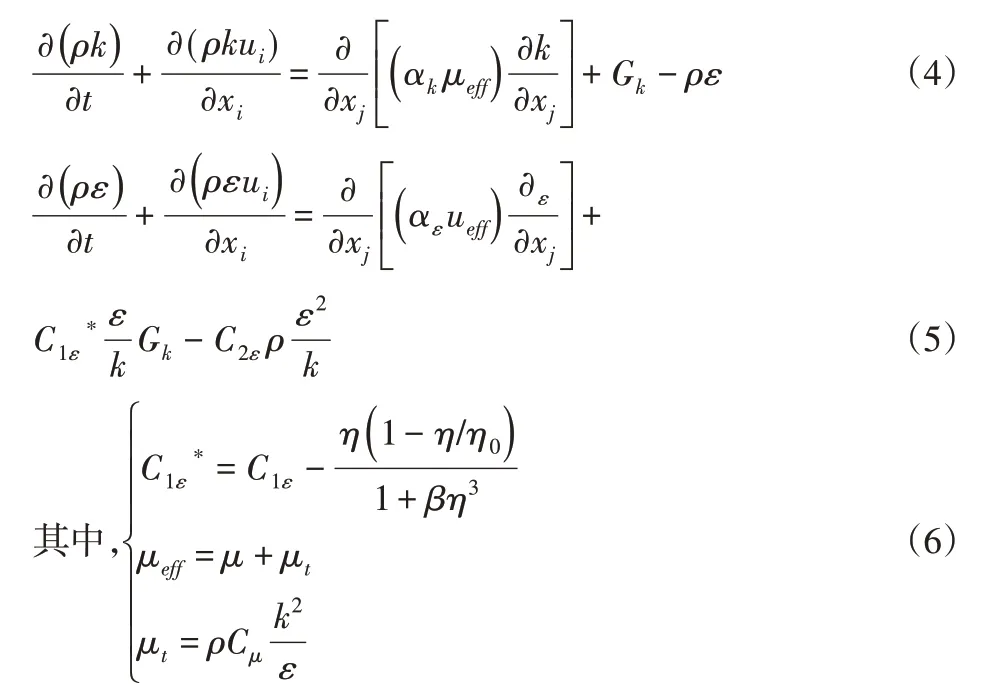
式中：Gk—由于平均速度梯度引起的湍动能产生项；μt—湍流粘性系数，αk、αε—湍动能k和耗散率ε的有效湍流普朗特数的倒数；C1ε、C2ε、Cμ、αk、αε—经验常数，C1ε=1.42，C2ε=1.68，Cμ=0.0845，αk=αε=0.7179。

RNG k −ε模型在ε方程中加了一个条件，为湍流普朗特数提供了一个解析公式，而标准k −ε 模型是用户提供的常数，且RNG理论提供了一个取决于正确对待近壁区域的解析公式，该公式考虑了低雷诺数流动黏性，这些特点使得RNG k −ε模型具有更高的精度［11］。

3.3 数值计算方法与边界条件

本次微风发电模型的数值计算选择三维双精度求解器，以提高求解精度，为提高求解速度，采用并行计算，在求解器中选择隐式（implicit）和稳态（steady）求解，且基于压力的求解器，速度采用绝对速度（Absolute）。风速为3m/s 时的雷诺系数Re远大于4000，所以流体的流动状态为高雷诺数流动，湍流模型采用RNG k −ε模型，近壁面处理采用标准壁面函数。

采用有限体积法对计算区域和控制方程进行离散化，得到离散方程，用有限体积法导出的方程可以保证守恒特性，其中动量、湍动能和湍流耗散率的离散格式均采用二阶迎风格式，对离散方程进行求解采用分离解法，采用默认的亚松弛因子，压力速度耦合算法为SIMPLE 算法，即求解压力耦合方程组的半隐式方法，其边界条件如下：

速度入口：流域入口面为速度入口边界，为验证微风及高速风对模型同样适用，采用不同来流风速对三维模型进行数值模拟，来流风速V0变化为2.5m/s，5.0m/s，7.0m/s，10m/s；

速度出口：流域出口面选择自由出流，设置为outflow；

微风发电装置模型为壁面边界，绝对静止且无滑移边界条件；流域其余外壁为对称边界。

监视器的设置，监测残差值在迭代计算过程中，当各个物理变量的残差值都达到收敛标准时，计算就会发生收敛。Fluent默认的收敛标准是：当所有变量的残差值都降到低于10−3数量级时，就认为计算收敛。采用标准化方法进行初始化求解，计算起始于入口边界，迭代次数设置为1000，然后开始迭代求解。

3.4 结果与分析

3.4.1 不同风速下流场中心面速度场分布

四种不同来流风速时流场中心面的速度分布云图，如图5所示，模型在不同来流风速下的计算结果，如表1所示。

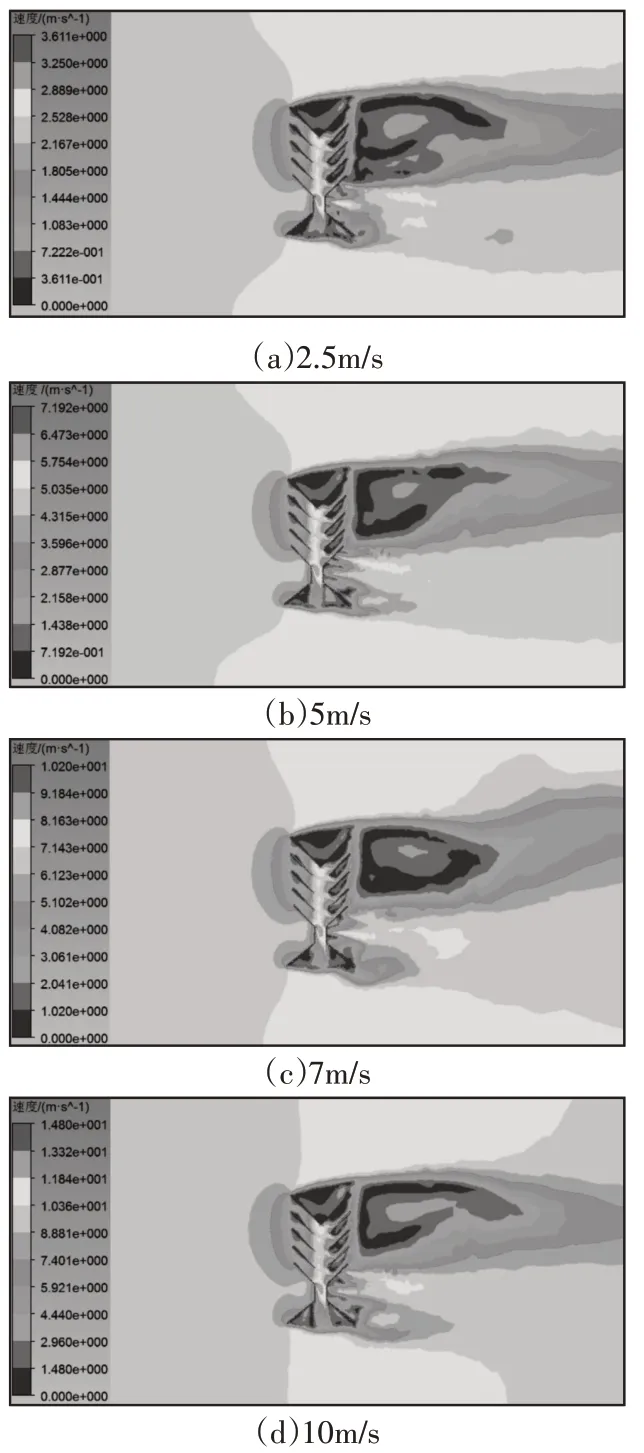
图5 不同风速下流场中心面流速分布Fig.5 Flow Velocity Distribution at the Center of the Flow Field at Different Wind Speeds

由图5与表1可以得出，由于存在阻力作用，微风发电模型入口处风速较来流风速有所降低，但由喉管处风速可知，该模型确实具有提高流速的效果，相比来流风速，速度增益为1.38−1.42，且随来流风速的增大而增大但幅度不大。由喉管处的速度分布可知，喉管中间部位的流速较高，由于管道对气流的粘滞性，喉管近壁面区域流速明显降低。因此，在喉管内安装风力机叶片应避开低流速区域。

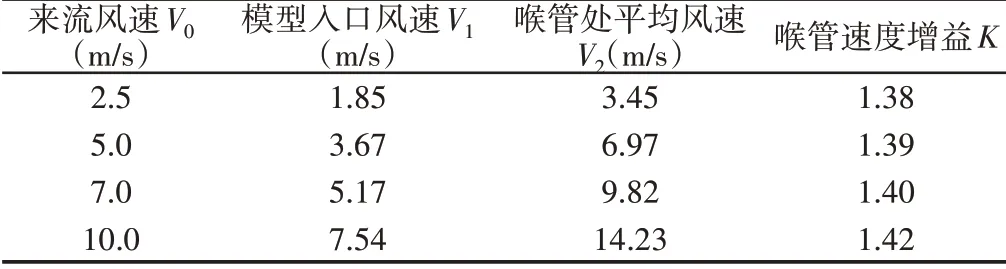
表1 不同来流风速的计算结果Tab.1 Calculation Results of Different Incoming Wind Speeds

3.4.2 不同风速下流场中心面压力场分布

四种不同来流风速时流场中心面的压力分布云图，如图6所示。由图6可以看出，模型迎风方向为正压力，背风方向为负压力，且都随来流风速的增大而增大，由于来流方向的气流受到模型的阻力作用，将风压由动压转为静压，压力达到最大值，模型内部的静压与模型外部静压相比要小，且喉管处出现负压值，由此产生抽吸作用使得模型内部的流量及风速增大，达到发电功率增加的目的。

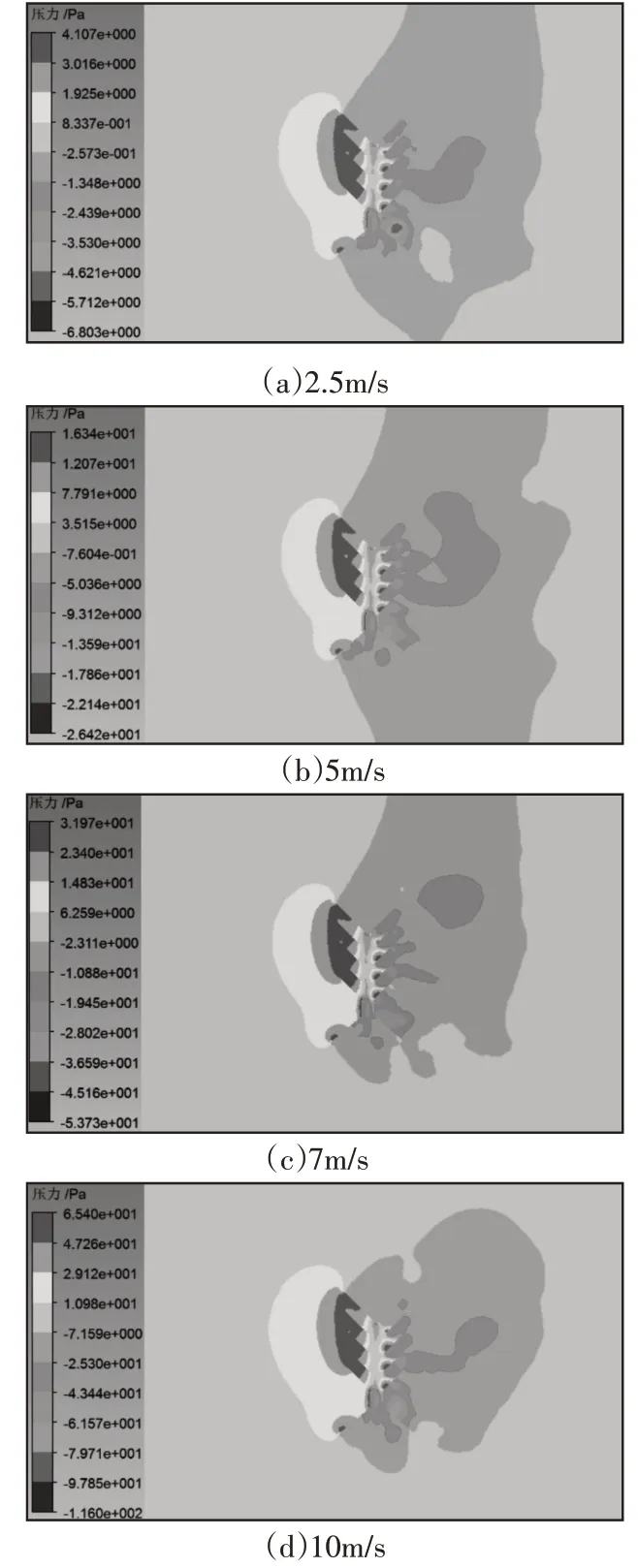
图6 不同风速下流场中心面压力分布Fig.6 Pressure Distribution at the Center of the Flow Field at Different Wind Speeds

4 高效微风发电装置的风洞试验

4.1 风洞与测试设备

为验证数值模拟方法的有效性，对所研究的微风发电装置进行风洞试验。本次风洞试验是在河北铁道大学风工程研究中心的串联双试验段回流边界层风洞，其低速试验段宽4.4m，高3.0m，长24.0m，最大风速大于30.0m/s，高速试验段宽2.2m，高2m，长5.0m，最大风速大于80.0m/s。低速验段流场达到优秀边界层风洞流场标准，高速试验段流场达到优秀工业空气动力学风洞标准。低速试验段内配备有三维移测架系统，可在24m试验段内通长和横向、纵向移动，在连续吹风状态下完成风场的测量。本次试验在低速试验段进行，其速度不稳定性小于等于0.6%，速度场不均匀性小于等于0.4%，湍流强度小于等于0.4%。

测试设备：风速测量采用澳大利亚TFI 公司生产的压力探头，测量不同工况下的风速。压力测量采用美国PSI公司生产的压力扫描阀和数据处理软件组成风压测量、记录和处理系统［12］。

4.2 试验方法

风洞试验与试验模型，如图7所示。风洞控制系统，如图8所示。将试验模型固定于低速段的转盘上，在模型前方设置皮托管风速仪，用来监测来流风场风速，本次试验设定来流风速为（2.5~10）m/s。

图7 风洞试验与试验模型Fig.7 Wind Tunnel Test and Test Model

图8 风洞控制系统Fig.8 Wind Tunnel Control System

在模型入口中间位置、喉管位置设置测速压力探头以及测压孔，来测量速度变化和压力变化，测试设备安装完成后，利用控制系统开始风洞试验。

4.3 试验结果与分析

对数值模拟计算获得的喉管速度增益K和模型进出口压差P与试验值进行比较，绘制出的来流风速V0与喉管速度增益K、模型进出口压差P的关系曲线，如图9、图10所示。

从图9和图10可以看出，风洞试验测试结果比数值模拟计算值略大，且误差保持在10%以内，其原因是数值模拟对模型的简化使其存在一定误差。数值模拟计算的喉管速度增益K和模型进出口压差P与试验值均随着来流风速V0的增加呈上升趋势，其中试验测试的喉管速度增益K约1.4，与数值模拟计算值基本一致，验证了数值模拟的有效性，进一步验证了该微风发电装置能够有效提高来流风速，提高发电功率。

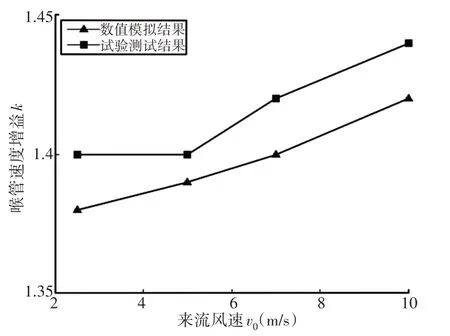
图9 V0−K关系曲线Fig.9 V0−K Relationship Curve

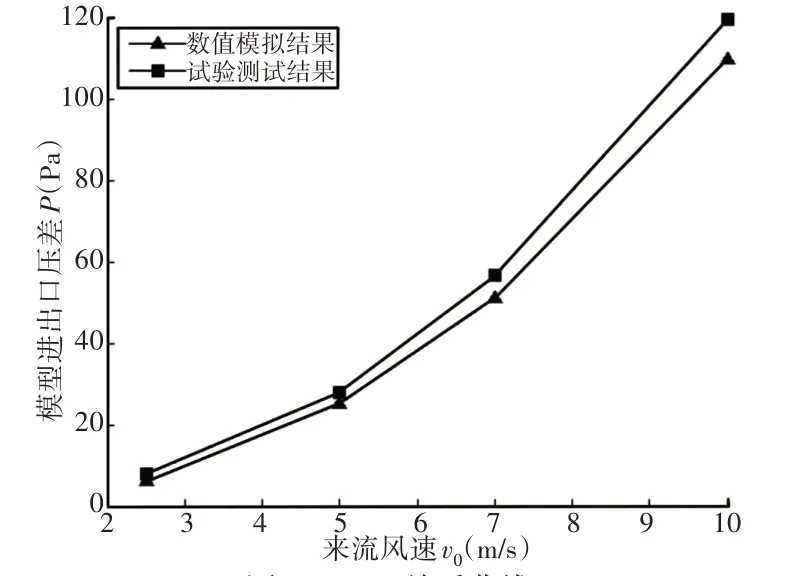
图10 V0−P关系曲线Fig.10 V0−P Relationship Curve

5 结论

（1）设计了一种高效微风发电装置，其发电原理依据“文丘里效应”提高了来流风速，万向迎风结构消除了传统风力机的对风时间，增加了多变风向环境下的适应性，提高工作效率。

（2）通过Fluent仿真分析可知，相对于来流风速，喉管处速度增益在（1.38~1.42），且随来流风速增大而增大，提速效果较好，在低风速地域也可以充分利用风能，对于3m/s以下的微风可有效提高到工作风速，大大增加了发电功率。

（3）对微风发电装置进行风洞试验，对比数值模拟结果与试验结果表明，微风发电装置数值模拟与试验所得速度和压力数据基本一致，速度增益均达到1.4左右，说明设计的高效微风发电装置在提速、提效方面具有准确性和可靠性。