
翰墨点睛:国投坐标
栏头合书:惠民、乔杨
国土名片网钤印:王子廬
插播导读:国土名片网小编芬儿、新宇、张扬、李浩
坐标基准间的坐标转换
《安徽建筑》杂志 2020年10期 作者:丁爱民 (安庆市勘察测绘院,安徽 安庆 246000)
0 前言
坐标基准是测绘工作的空间起算依据,不仅为空间地理信息描述提供起算原点和起算面,也是确定空间地理信息的几何形态和时空分布规律的基础。坐标系统之间的差异主要来自于坐标系统的定义不同,具体表现为坐标系原点、坐标轴指向和尺度因子的差异。目前常用的坐标系统有2000国家大地坐标系、1980西安坐标系和1954北京坐标系。
随着2000国家大地坐标系(CGCS2000)的实施,将有多源、多尺度的海量空间地理信息数据需要统一到新的测绘基准,以满足城市建设和管理对测绘地理信息产品的需求。在将现有成果转换至CGCS2000的具体实践中,众多学者对三维七参数法、平面四参数法等坐标转换方法开展了深入研究,而针对不同区域、不同坐标转换模型的适用性分析不够。因此,研究一种满足一定精度要求的转换方法,实现不同参考椭球基准下的坐标转换,对实际工作具有指导意义。
1 坐标转换原理与方法
坐标转换包括坐标系转换和坐标基准转换。坐标系转换是基于同一参考椭球下的不同表现形式的坐标转换,如空间直角坐标(X,Y,Z)与大地坐标(大地纬度B,大地经度L,大地高H)的相互转换、高斯平面直角坐标(X,Y)与大地坐标(B,L)的相互转换;坐标基准转换是基于不同参考椭球下的坐标转换,如不同空间直角坐标系的转换、不同大地坐标系的转换和不同平面坐标系的转换。根据转换形式,又可分为二维坐标转换和三维坐标转换。常用的坐标转换模型有基于空间坐标的布尔莎模型、基于大地坐标的三维七参数模型、基于平面坐标的平面四参数模型等。
不同坐标系坐标转换的实现是根据同时拥有两种坐标系坐标的大地点(重合点)的条件下,选择适当的重合点,利用所选重合点两种坐标系的坐标,采用适当的坐标转换模型,运用最小二乘法计算坐标转换参数,再通过坐标回代求得所求坐标系的坐标。
坐标转换通常有两种方法:一是整体转换法,整个区域计算一套转换参数;二是分区转换法,当转换区域较大时,为保证转换精度,将整个转换区域划分成若干个分区,分别对各分区计算转换参数。在计算各分区转换参数时,为了保持各分区在接边处转换参数的连续性,需要各分区之间相互重叠一部分重合点并重复使用以求取转换参数。
坐标转换的精度除取决于坐标转换的数学模型和求解转换参数的重合点坐标精度外,还与重合点的数量、几何形状结构有关。为满足规范要求,必须选取高等级、高精度且分布均匀的点作为坐标转换的重合点;重合点的分布要覆盖整个转换区域且尽量分布均匀,特别要注意转换区域周边覆盖;重合点的数量不得少于5个。同时应对参与解算转换参数的重合点进行准确分析、筛选、试算,剔除大于3倍中误差的粗差点,采用不含粗差且具有一定密度的重合点解算转换参数,直到满足精度要求为止。评定转换参数的精度包括内符合精度和外符合精度,用参与参数计算的重合点坐标残差计算内符合精度,选择部分未参与参数计算的重合点作为外部检核点,用转换参数计算这些点的坐标与已知坐标比较进行外部检核,得到坐标残差计算外符合精度。用于检核坐标转换精度的外部检核点不应少于6个。
2 坐标转换模型
2.1 布尔莎模型(三维七参数)
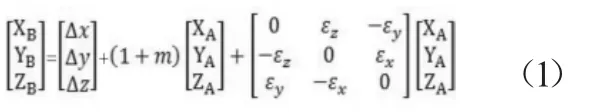
式中:(XAYAZA)T为某点在空间直角坐标系A的坐标,(XBYBZB)T为该点在空间直角坐标系B的坐标,(Δx Δy Δz)T为3个平移参数;(εxεvεz)T为3个旋转参数;m为尺度变化参数。
该模型中含有7个转换参数,为了求得这7个参数,至少需要3个重合点,当多于3个重合点时,可按最小二乘法求得7个参数的最或是值。
2.2 平面四参数模型(二维四参数)
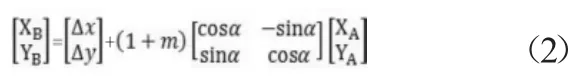
式中:2 个平移参数 Δx、Δy,1 个旋转参数α和1个尺度变化参数m。
采用平面四参数模型共有4个转换参数,至少需要2个重合点,当多于2个重合点时,可按最小二乘法求得4个参数的最或是值。
2.3 转换参数精度评定
坐标转换精度是通过求取转换参数的重合点的残差中误差体现的。转换精度依据下式计算:

对转换参数进行精度的检验、评定主要包括以下两个方面:参与参数计算的重合点的内符合精度;未参与参数计算的外部检核点的外符合精度。
3 工程案例
将安庆市1954年北京坐标系成果转换到CGCS2000国家大地坐标系,使用工具软件为安庆市2000国家大地坐标系转换软件,其功能主要分为7大模块,包括坐标转换参数求解、设置转换参数、DLG数据转换、DEM数据转换、DOM数据转换、字符串格式数据转换和常用软件包(高斯投影正反算(X,Y)与(B,L)相互转换;3°、6°、任意带投影换带计算;空间大地坐标(B,L,H)与空间直角坐标(X,Y,Z)相互转换)。该软件支持1954年北京坐标系、1980西安坐标系、CGCS2000坐标系之间的相互转换;支持多种转换方法,包括平面四参数、三维七参数、布尔莎三维七参数等;支持点数据、图形数据等对象以及多种数据格式的文件。
3.1 转换精度分析
①设置计算转换参数的重合点相邻点对平均间距10km,选取市域125个C级和D级GPS点以及224个实测CGCS2000坐标的特征点作外部检核,分别采用布尔莎模型和平面四参数模型进行试算求取转换残差,统计按两种模型得到的平面坐标分量残差及点位中误差(单位m)分布区间,并进行对比分析。
采用布尔莎模型转换:平面坐标x分量转换精度为0.008m,平面坐标y分量转换精度为0.009m,平面点位中误差0.012m。平面坐标x分量残差绝对值最大值0.061m,平面坐标y分量残差绝对值最大值0.043m。平面点位中误差最大值为0.055m。平面点位中误差分布见图1。
采用平面四参数模型转换:平面坐标x分量转换精度为0.013m,平面坐标y分量转换精度为0.008m,平面点位中误差0.015m。平面坐标x分量残差绝对值最大值0.019m,平面坐标y分量残差绝对值最大值0.019m。平面点位中误差最大值为0.027m。平面点位中误差分布见图2。
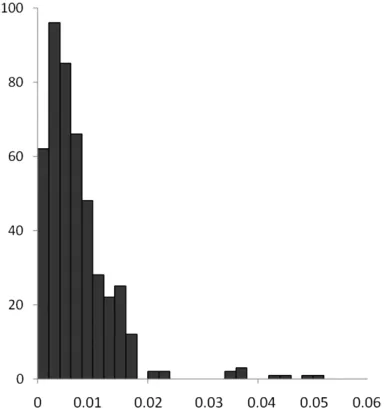
图1 布尔莎模型(10km)平面点位中误差分布直方图
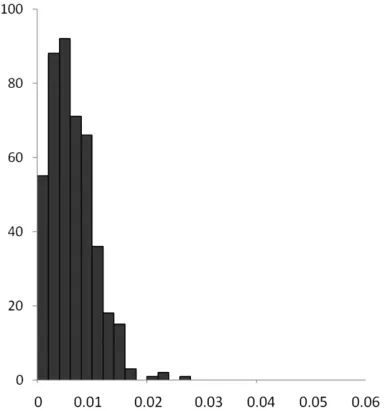
图2 平面四参数模型(10km)平面点位中误差分布直方图
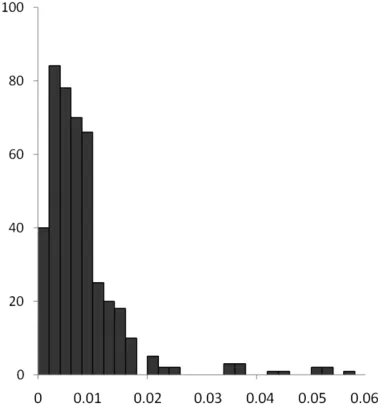
图3 布尔莎模型(15km)平面点位中误差分布直方图
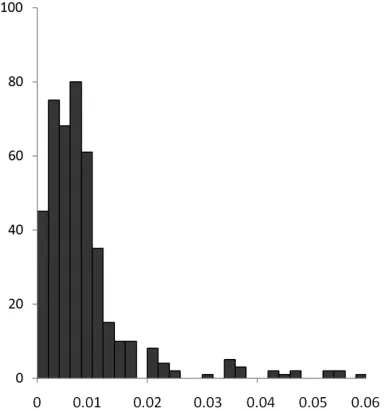
图5 布尔莎模型(20km)平面点位中误差分布直方图
②设置计算转换参数的重合点相邻点对平均间距分别为15km、20km时,按两种模型计算转换残差得到的平面点位中误差分布见图3~图6。
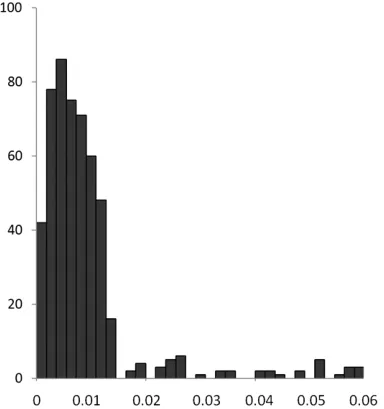
图6 平面四参数模型(20km)平面点位中误差分布直方图
从平面点位中误差分布直方图可以看出,99%的转换误差分布在3倍中误差以内,小于图上0.1mm,个别山地转换精度大于5cm,主要集中在偏离中央子午线较远的山地,但是不影响整体转换精度评价。
随着转换区域的增大,采用布尔莎模型转换精度变化不大,而平面四参数模型转换精度衰减显著,其原因是投影变形所致。
3.2 分析结论
①平面四参数模型属平面坐标系间的二维相似变换,未考虑椭球曲面影响,适用于投影变形小的局部区域坐标转换。其转换精度能够满足1∶500比例尺的图形转换,布尔莎模型是空间直角坐标系间基于不同椭球的三维转换,适用于较大区域的坐标转换,其转换精度能够满足1∶1000比例尺及更小的图形转换。
②当转换区域较大时,为保证必要的转换精度,坐标转换可采取两种方法,一是划分转换区域分别转换,二是在三维七参数模型中增加椭球长半轴和扁率变化参数进行约束。
4 结语
坐标基准转换是不同椭球间的坐标转换。在实际应用中,要综合考虑待转换的两个坐标系的基本信息、转换区域与地图投影中央子午线的距离、区域大小、重合点的数量及分布等情况,选择适宜的坐标转换模型,对重合点的选择方案以及转换模型进行反复验证,确定转换参数,提高坐标转换精度。
